Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.4 Nomor 7 Halaman 256 Ada Teori dan Caranya

TRIBUNJOGJA.COM - Berikut kunci jawaban dan cara mengerjakan soal Latihan 4.4 Nomor 7 di Buku Matematika SMP Kelas 9 halaman 256.

Buku yang digunakan dalam artikel Tribunjogja.com ini adalah Buku Matematika SMP Kelas 9 Kurikulum 2013 Edisi Revisi 2018.

Buku tersebut diterbitkan oleh Pusat Kurikulum dan Perbukuan, Badan Penelitian dan Pengembangan (Balitbang), Kementerian Pendidikan dan Kebudayaan (Kemendikbud).

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 7 Halaman 256

7. Perhatikan gambar.
a. Hitunglah panjang EB
b. Hitunglah panjang CE

Kunci Jawaban dan Cara Mengerjakannya :

Sebelum menjawab, mari kita ingat kembali materi kesebangunan dua segitiga yang termuat dalam Buku Matematika Kelas 9 halaman 249.

Syarat Segitiga Sebangun

Dua segitiga dikatakan sebangun apabila memenuhi syarat-syarat berikut ini:

1) Perbandingannya ketiga pasangan sisi yang bersesuaian sama
2) Dua pasang sudut yang bersesuaian sama besar
3) Perbandingan dua pasang sisi yang bersesuaian sama dan sudut yang diapitnya sama besar.

Selain memahami syarat kesebangunan segitiga, mari kita ingat kembali teori sifat-sifat sudut.

Hubungan Antarsudut pada Dua Garis Sejajar

Melansir ulasan dari Supriaten, Guru SMP Negeri 5 Tanah Grogot, Paser, Kalimantan Timur, via Kompas.com, berikut hubungan dan sifat-sifat antarsudut dua garis sejajar yang dipotong garis transversal:

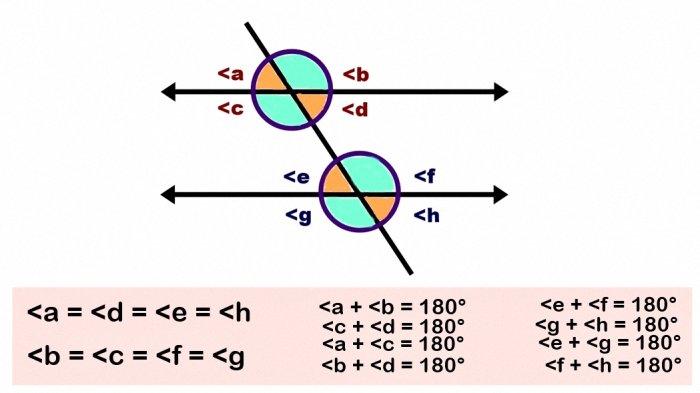
• Sudut sehadap sama besar
• Sudut dalam berseberangan sama besar
• Sudut luar berseberangan sama besar
• Sudut bertolak belakang sama besar
• Jumlah sudut dalam sepihak = 180°
• Jumlah sudut luar sepihak = 180°
• Jumlah sudut berpelurus = 180°

Dua teori yang dipaparkan di atas akan membantu kalian menjawab soal Latihan 4.4 Nomor 7 poin A dan B berikut ini.

a. Menghitung Panjang EB

Perhatikkan gambar di atas.

Dapat diketahui bahwa bangun ∆CAB sebangun dengan ∆CDE karena dua segitiga tersebut memenuhi syarat sudut bersesuaian sama besar.

• ∠ACB = ∠DCE karena keduanya berimpit
• ∠ABC = DEC karena keduanya sehadap
• ∠CAB = ∠CDR karena keduanya sehadap

Karena ∆CAB sebangun dengan ∆CDE maka perbandingan panjang sisi-sisi yang bersesuaian sama besar.

Dengan begitu, kita bisa mencari panjang sisi EB menggunakan rumus perbandingan sisi bersesuaian.

CB : CE = AB : DE
(EB + CE) : CE = AB : DE
(EB + 6 cm) : 6 cm = 7 cm : 5 cm
EB + 6 cm = 7/5 x 6 cm
EB + 6 cm = 42/5
EB + 6 cm = 8,4 cm
EB = 8,4 cm - 6 cm
EB = 2,4 cm

b. Menghitung Panjang CE

Perhatikkan gambar di atas.

Dapat diketahui bahwa bangun ∆ABC sebangun dengan ∆EBD karena dua segitiga tersebut memenuhi syarat sudut bersesuaian sama besar.

• ∠CBA = ∠DBE karena keduanya berimpit
• ∠ACB = ∠EDB karena sudah diketahui dalam soal, terlihat ada tanda titik
• ∠CAB = ∠DEB karena jumlah sudut pada segitiga adalah 180° dan sudah diketahui dua pasang sudut bersesuaian lainnya sama besar sehingga sudah jelas bahwa ∠CAB = ∠DEB.

Telah terbukti ∆ABC sebangun dengan ∆EBD maka perbandingan panjang sisi-sisi yang bersesuaian sama besar.

Dengan begitu, kita bisa mencari panjang sisi CE menggunakan rumus perbandingan sisi bersesuaian.

CB : DB = AB : EB
(CE + 4 cm) : 6 cm = (2 cm + 6 cm) : 4 cm
(CE + 4 cm) : 6 cm = 8 cm : 4 cm
(CE + 4 cm) : 6 cm = 2
CE + 4 cm = 2 x 6 cm
CE + 4 cm = 12 cm
CE = 12 cm - 4 cm
CE = 8 cm

Baca juga: Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.4 Nomor 1 Halaman 254 dan Teorinya

Baca juga: Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.4 Nomor 6 Halaman 255 dengan Cara Mengerjakan

Itulah kunci jawaban dan penjelasan cara mengerjakan soal Latihan 4.4 nomor 7 poin A dan B di Buku Matematika SMP Kelas 9 halaman 256.

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 1 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 2 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 3 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 4 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 5 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.4 Nomor 6 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.1 Nomor 1-14 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.2 Nomor 1-12 klik di sini

Kunci Jawaban Matematika Kelas 9 Latihan 4.3 Nomor 1-12 klik di sini

Disclaimer:

Kunci jawaban yang dibahas di artikel ini mengacu pada Buku Matematika Kelas 9 Kurikulum 2013 Edisi Revisi 2018 Khusus Guru dan perhitungan penulis Tribunjogja.com.

Artikel ini ditulis dengan tujuan memudahkan orangtua dalam memandu belajar anak di rumah.

Bagi siswa yang membaca kunci jawaban, ada baiknya berusaha mengerjakan semampunya terlebih dahulu. 

Setelah mengerjakan sendiri, silakan mengoreksi hasil pekerjaan dengan melihat kunci jawaban.

Tribunjogja.com tidak bertanggung jawab apabila kunci jawaban Buku Matematika SMP Kelas 9 dalam artikel ini berbeda dengan kunci jawaban versi guru di sekolah masing-masing.

Jika ada yang ingin ditanyakan tentang pelajaran Matematika Kelas 9, jangan ragu bertanya atau menghubungi guru mata pelajaran yang bersangkutan di sekolah masing-masing. 

Selamat belajar… Semangat! (Tribunjogja.com/ANR)