Rumus Hitung Mean, Median, Modus Lengkap Dengan Contoh Soalnya

TRIBUNJOGJA.COM - Di bangku sekolah dalam pelajaran matematika pasti  akan mempelajari mean, median dan modus.

Untuk mempelajari cara menghitung mean, median, modus, akan mempermudah untuk mendapatkan gambaran lebih jelas mengenai keseluruhan data.

Sebelum melihat rumus mean, median, dan modus, tentunya anda harus mengerti definisi dahulu

Baca juga: Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.4 Nomor 11 Halaman 257 den Langkah-langkahnya

Definisi mean, median, dan modus. Dilansir oleh TribunPontianak.com

Mean adalah nilai rata-rata yang didapatkan dari hasil penjumlahan seluruh nilai dari masing – masing data, kemudian dibagi dengan banyak data yang ada

Median adalah nilai tengah dari kumpulan data yang telah diurutkan, apabila jumlah data ganjil maka nilai median ialah satu nilai yang berada di tengah urutan, namun apabila jumlah data genap maka mediannya adalah hasil pejumlahan dua nilai yang berada ditengah urutan data, kemudian hasilnya dibagi dua.

Modus merupakan data atau nilai yang paling sering muncul atau yang memiliki jumlah frekuensi terbanyak.

Setelah paham dari definisi median, mean dan modus, selanjutnya simak rumus dari setiap model yang ada untuk menyelesaikan soal dan jawaban

Rumus mean

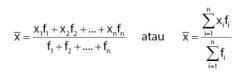
rumus median 

rumus modus

Keterangan

tb = tepi bawah kelas median

f1 = selisih dari frekuensi kelas modus dengan frekuensi sebelum kelas modus

f2 = selisih dari frekuensi kelas modus dengan frekuensi setelah kelas modus

p = panjang kelas interval

Contoh soal 1

Ahmad mengerjakan tes matematika sebanyak 7 kali dan mendapatkan nilai sebagai beriku 6, 6, 7, 7, 8, 9, 7. Berapakah nilai rata – rata tes matematika Ahmad?

Pertama –pertama jumlahkan seluruh nilai yang ahmad dapatkan

6 + 6 + + 7 + 7 + 8 + 9 + 7 = 50

Jumlah nilai Ahmad dibagi dengan frekuensi tes yaitu

50 : 7 = 7,14

Baca juga: Kunci Jawaban Buku Matematika SMP Kelas 9 Latihan 4.4 Nomor 10 Halaman 256 dan Penjelasannya

Contoh soal 2.

Diketahui sebuah data adalah sebagai berikut

3, 5, 2, 7, 9, 1, 7, 5, 3, 8, 10, 12, 5

Berapa nilai media dari data diatas?

Hal pertama yang dilakukan adalahan mengurutkannya dari terkecil hingga terbesar, hasilnya adalah 1, 2, 3, 3, 5, 5, 5, 7, 7, 8, 9, 10, 12.

Setelah mengetahui jumlah data, yaitu ada sebanyka 13 data. Karena jumlah data ganjil maa kita bisa langsung menentuka median

Caranya adalah dengan melihat nilai yang berada di tengah,yaitu nilai urutan ketujuh, jadi, median dari data tersebut adalah 5

Jika ingin mengetahui cra menghitung cepat, kita tinggal menghitung dengan rumus berikut:

Median (Me) = (jumlah data + 1) : 2

Me = ( 13 + 1 : 2

Me = 14 : 2 = 7

Nilai ke-7 data dari atas adalah 5.

Contoh soal 3

Diketahui sebuah data tunggal 2, 4, 6, 7, 7, 8, 9, 10. Berapakan modusnya?

Modus dari data di atas adalah 7 sebab muncul 2 kali, lebih banyak dibandingkan yang lain.

Ex ( MG Mubarok Yahya )