Pengetahuan Umum
Rangkuman Matematika SMP 7 Materi Bab 5 Bangun Datar Titik, Garis, Geometri dan Lingkaran 1.2
Rangkuman Matematika SMP 7 Materi Bab 5 Bangun Datar Titik,Garis,Lingkaran,dan Geometri
Penulis: Tribun Jogja | Editor: Joko Widiyarso
TRIBUNJOGJA.COM-Berikut Rangkuman Matematika SMP 7 Materi Bab 5 Bangun Datar Titik,Garis dan Lingkaran
1. Jarak Antara Dua Titik
Pengertian: Jarak antara dua titik dalam bidang datar adalah panjang garis lurus yang menghubungkan kedua titik tersebut.
Rumus: Jika dua titik A(x1,y1)dan B(x2,y2) diberikan, jarak d antara keduanya dapat dihitung menggunakan
d=√(x2-x1)2+(y2-y1)2
2. Jarak Antara Titik dan Garis
Pengertian: Jarak antara sebuah titik dan garis adalah panjang garis lurus dari titik tersebut ke garis, yang selalu diukur pada garis tegak lurus terhadap garis tersebut.
Rumus: Jika garis dinyatakan dalam bentuk Ax+By+C=0 dan titik P(x0,y0) jarak d antara titik dan garis dapat dihitung dengan rumus:

3. Jarak Antara Dua Garis Sejajar
Pengertian: Jarak antara dua garis sejajar adalah panjang garis tegak lurus yang menghubungkan dua garis tersebut. Jarak ini tetap dan sama di sepanjang kedua garis.
Rumus: Jika dua garis sejajar dinyatakan dalam bentuk Ax+By+C1=0 dan Ax+By+C2=0, jarak d antara kedua garis dapat dihitung dengan rumus:
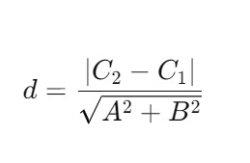
1.. Juring
Arti: Juring adalah daerah yang dibatasi oleh dua jari-jari (garis yang menghubungkan titik pusat lingkaran dengan dua titik pada lingkaran) dan busur di antara kedua jari-jari tersebut.
Cara Menyatakan: Juring yang dibatasi oleh titik A dan B dapat dinyatakan sebagai AOB di mana O adalah titik pusat.
2. Sudut Tengah
Arti: Sudut tengah adalah sudut yang dibentuk oleh dua jari-jari lingkaran yang berasal dari titik pusat dan mengarah ke dua titik pada lingkaran.
Cara Menyatakan: Jika A dan B adalah dua titik pada lingkaran dan O adalah pusat lingkaran, sudut tengah dapat dinyatakan sebagai ∠AOB
3. Garis Lurus Tegak Lurus
Arti: Dua garis atau segmen garis dikatakan tegak lurus jika mereka bertemu membentuk sudut 90 derajat (sudut siku-siku).
Cara Menyatakan: Jika garis lll dan garis mmm tegak lurus, dapat dinyatakan sebagai l⊥ml
4.Titik Pusat
Arti: Titik pusat adalah titik yang terletak di tengah lingkaran, di mana semua jari-jari dari lingkaran tersebut berujung.
Cara Menyatakan: Titik pusat lingkaran biasanya dinyatakan dengan huruf besar, misalnya O.
Arti Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang bersentuhan dengan lingkaran pada satu titik saja. Titik di mana garis tersebut menyentuh lingkaran disebut titik singgung.
Sifat-sifat Garis Singgung Lingkaran
Tegak Lurus terhadap Jari-jari:
Garis singgung pada titik singgung akan tegak lurus terhadap jari-jari yang menghubungkan pusat lingkaran dengan titik singgung tersebut. Jika O adalah pusat lingkaran dan T adalah titik singgung, maka OT⊥ garis singgung.
Hanya Satu Titik Sentuh:
Garis singgung hanya menyentuh lingkaran di satu titik, sehingga tidak ada titik lain di mana garis tersebut berpotongan dengan lingkaran.
Garis Singgung pada Lingkaran dalam:
Jika terdapat lingkaran dalam (lingkaran yang terletak di dalam lingkaran lain), garis singgung dari lingkaran luar ke lingkaran dalam juga akan memiliki sifat yang sama, yaitu menyentuh lingkaran dalam di satu titik.
Jarak dari Pusat ke Garis Singgung:
Jarak dari pusat lingkaran ke garis singgung sama dengan panjang jari-jari lingkaran.
Contoh Penggunaan
Garis singgung sering digunakan dalam berbagai aplikasi geometri, fisika, dan teknik, seperti dalam analisis gerakan, desain mesin, dan lain-lain.
Selamat Membaca ( MG Tiara Ning Tyas )
| Pengertian, Jenis, Unsur, Ciri Berita: Rangkuman Materi Bahasa Indonesia SMA/SMK XI Bab 2 |

|
|---|
| Rangkuman Materi Bahasa Indonesia SMA/SMK XI Bab 5 Perbedaan Puisi,Prosa,Dan Drama |

|
|---|
| Rangkuman Materi Bahasa Indonesia SMA/SMK XI Bab 4,Unsur-Unsur Puisi: Intrinsik dan Ekstrinsik |

|
|---|
| Rangkuman Materi Bahasa Indonesia SMA/SMK XI Bab 4 |

|
|---|
| Rangkuman Materi Bahasa Indonesia SMA/SMK XI Bab 3 |

|
|---|
















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.